Modern Rifling Twist Realities

To understand the latest information on rifling twist, we need to understand why bullets fly point-forward. The spin imparted by rifling gives a bullet gyroscopic stability, the force that allows a spinning top to remain upright – but unlike a top, a bullet flies through the atmosphere, sometimes at speeds over 4,000 feet per second. As a result, air pressure pushes against the front of the bullet, like wind against a soda can lying in the street – a strong enough wind overcomes the can’s weight, sending it tumbling across the pavement. Much the same occurs when the “wind” on a bullet overcomes its gyroscopic stability; instead of flying point-on, the bullet tumbles through the air.

Slower rifling twists will stabilize long, high-BC bullets in the thinner air of higher elevations. This E.R. Shaw 6.5-06’s barrel has a relatively slow 1:9 twist but stabilized a 140-grain Berger VLD very well at 7,000 feet above sea level.

Some humans have a compulsion to convert almost any aspect of the universe into a mathematical formula. This often causes other humans to fall asleep, but math makes constructing many nifty things possible, including pickup trucks, telescopic sights and rifle barrels. Consequently, many formulas have been devised to predict the rifling twists required to keep bullets point-forward. The best known is the Greenhill formula, developed in 1879 by a British mathematician, Sir Alfred George Greenhill.

Even though electronic anemometers, like this Minox variant, can measure wind speed where a shooter stands, both wind velocity and direction can vary over longer distances.

Greenhill empirically developed a twist formula through testing bullets fired in different twists: Multiply bullet diameter by 150, then multiply the ratio of bullet diameter divided by bullet length. The result is the “correct” rifling twist, expressed in how many inches a bullet travels down the bore during one revolution. As an example, using a .458-caliber, 500-grain, roundnose bullet measuring 1.25 inches long: .458 x 150 x (.458 ÷ 1.25) = 25.17 inches. Thus a rifling twist of about one turn in 25 inches (1:25) will stabilize this bullet.

The formula worked pretty well with the blunt, all-lead bullets universal in Greenhill’s day, though slight modifications were often made after the appearance of smokeless powder and jacketed bullets. Some rifle enthusiasts still use the formula, but it’s also responsible for the misconception that a given bullet will always be stabilized by a certain twist rate. This isn’t true, because air varies considerably in density due to temperature, elevation and humidity, resulting in variations in air pressure on the front of a bullet.

Colder air is far denser than warmer air and at higher elevations is much thinner than at sea level. Humidity plays such a minor role it can be ignored except at very long ranges – although, unlike many people assume, “wet” air is actually less dense that dry air. This is because water molecules (H2O) contain two hydrogen atoms and one oxygen atom, and hydrogen is lighter than oxygen.

The original rifling twist of most military 6.5mm cartridges was around 1:8, the twist of the Lilja barrel on this custom 6.5x55. Even today’s lighter 6.5mm bullets still shoot well when “overstabilized.”

In denser air, a bullet may not stabilize when shot in a certain rifling twist but may in thinner air. The Greenhill formula doesn’t include air density, perhaps because it was devised from observations in relatively cool, low-elevation England, so any change in atmospheric pressure was likely to result in thinner air.

Many shooters also believe bullet weight is the major factor in rifling twist, because bullet manufacturers often recommend a specific twist rate for bullets of certain weights. In reality, bullet length is most important, the reason the Greenhill formula also doesn’t include bullet weight, and why “lead-free” bullets won’t stabilize in twists that work for lead-core bullets of the same weight; lead-free bullets are longer, because their metals are lighter than lead.

Manufacturers normally recommend twist rates that stabilize a specific bullet in any environmental conditions. In warmer temperatures or at higher elevations, however, the same bullet will shoot well in slower twists. As a result, some handloaders decide the bullet company doesn’t know what it’s talking about (or they’re exceptional handloaders), because they can get the bullet to shoot well in slower twists. If they travel elsewhere, however, the bullet may not stabilize. This happened recently to a friend here in Montana who shoots at a local range 5,000 feet above sea level. He worked up an accurate handload in one of his rifles with a rifling twist slower than the manufacturer recommended for that bullet, then went to Texas to hunt feral pigs, where the elevation was 4,000 feet lower. Upon arrival he shot his rifle to check the scope’s zero, and the bullets scattered so widely some missed the paper. Luckily he’d brought two rifles, and the other shot fine.

While roundnose or flatnose bullets obviously result in higher air pressure against their front ends, they’re shorter than spitzers of the same weight, and their centers of mass are farther forward. As a result, they stabilize in slower twists and denser air than spitzers of equal length.

Roundnose bullets will stabilize in slower rifling twists better than spitzers, even though there’s more “air pressure” on their blunt noses, because they’re shorter than spitzers of the same weight, and their centers of mass are farther forward.

Many handloaders also believe faster muzzle velocity helps stabilize a bullet, partly because they’ve seen accuracy improve while adding more powder when working up a load. There’s a kernel of truth here, but in reality extra bullet spin created by more velocity only makes a tiny difference in bullet stability, because air pressure on the front of the bullet also increases. Plus, if a bullet’s being shot in what ballisticians call a “marginal” twist, it will destabilize in denser air, as my friend discovered in Texas. In reality, the primary reason more velocity often results is smaller groups is that modern powders are designed to burn most consistently at near-maximum pressures.

Smaller-caliber bullets require faster twists than larger-diameter bullets of the same length. This is why a .458 bullet that is 1.25 inches long stabilizes in a 1:25 twist, while a .277 spitzer of the same length normally requires a 1:10 twist.

All these factors have affected bullet and cartridge development since the first practical smokeless rifle powders appeared. Most early smokeless cartridges were military, beginning with France’s 8mm Lebel in 1886, and used heavy, roundnose bullets, apparently because the black-powder cartridges they replaced used heavy, roundnose bullets. The most prevalent bullet diameters were 6.5mm, 7mm, .30 and 8mm, and the long bullets required relatively fast rifling twists, around 1:8 in 6.5mm, 1:9 in 7mm and 1:10 in .30 and 8mm.

In 1898 Germany switched to a much lighter spitzer bullet in the 8x57, increasing range enormously. Other countries followed, but none changed the original rifling twists.

In contrast, during the same period, new sporting cartridges often featured relatively light bullets at high muzzle velocity, because the extra zip flattened trajectory over practical hunting ranges. One classic example is Savage’s .250-3000, introduced just before World War I. The .250’s original factory load featured an 87-grain spitzer at 3,000 fps in a 1:14 twist barrel, in order to avoid “overstabilizing” bullets.

The lightweight plastic tips of many modern high-BC bullets actually allow them to stabilize in slightly slower rifling twists than all-metal bullets of the same length.

Similarly, in 1925 Winchester came up with a brand-new bullet diameter for its brand-new .270 Winchester cartridge featuring a 130-grain bullet at a claimed 3,160 fps in a 1:10 rifling twist. Eventually most .25-caliber rifles also had 1:10 rifling twists, but 1:10 would not stabilize heavy spitzers with really high ballistic coefficients (BC) in either .25 or .270 caliber. This didn’t matter to hunters, because they rarely shot at ranges where higher BCs mattered – until laser rangefinders appeared on the civilian market in the late 1990s.

This is why 6.5mm and 7mm cartridges became far more popular among long-range hunters than .25s or .270s. Shooting “flat” was no longer necessary, because new scopes provided compensation for bullet drop. Instead, wind drift became the major variable, and heavy, high-BC bullets resist wind drift far more than lighter bullets at higher muzzle velocities. This is why very few truly high-BC .25 and .270 bullets are available: They won’t consistently stabilize in the standard 1:10 rifling twist.

It’s also the reason the predominant modern rifling-twist formula was devised specifically for high-BC boat-tail bullets. It was created by the late Don Miller, a retired rifle loony who had the desire, time and knowledge to fool around with twist numbers. I first met Don years ago at the annual SHOT Show, because he was interested in a couple of my simplistic ballistic formulas.

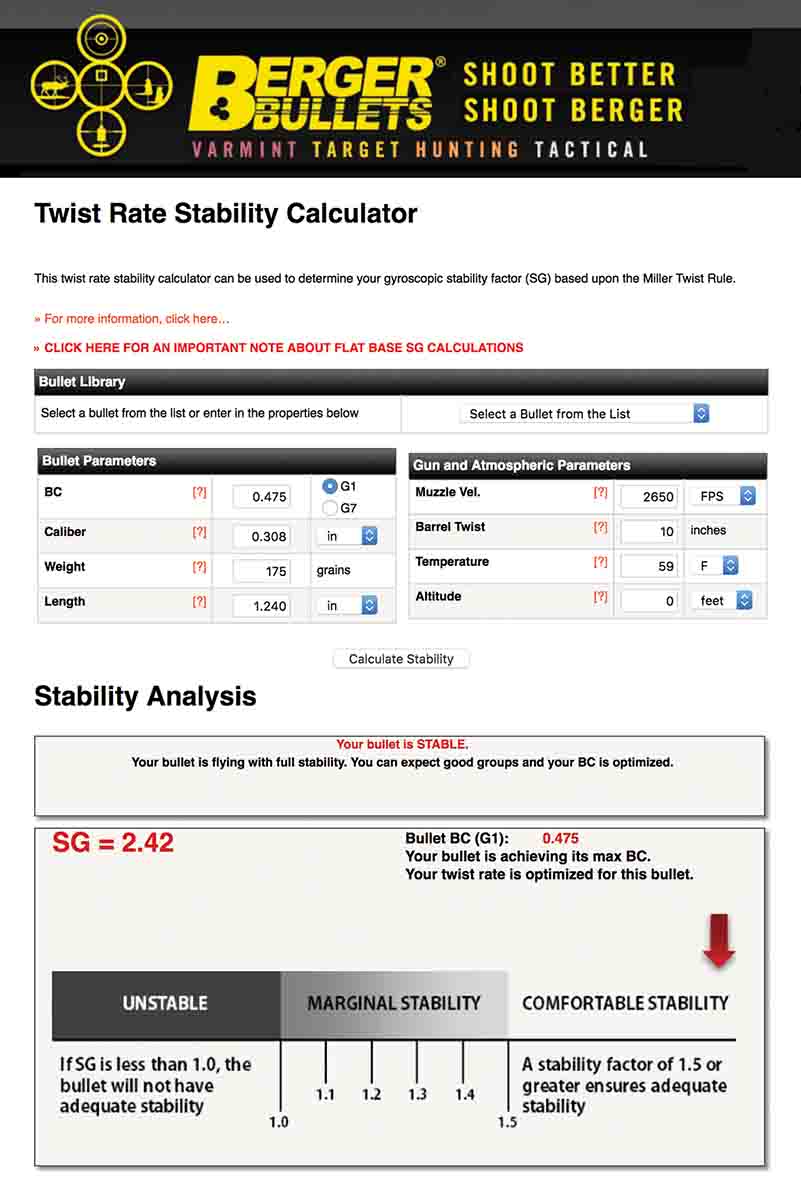
During our conversation, Don gave me a copy of an article he’d written on his new twist formula, which became the basis for the formulas used by companies involved in long-range shooting, including Berger Bullets and JBM Ballistics. Though the Miller formula is far more complex than Greenhill’s, it can still be worked on a pocket calculator. (If I can do it, many people can.) The easiest method is to use the Internet, logging onto www.bergerbullets.com or www.jbmballistics.com and plugging the numbers into the online formulas (see sidebar).

I’ve been using the Miller formula for at least a decade now, and due to living in Montana, where both elevation and temperature vary considerably, I can testify it’s very accurate, but any potential user should know some other details.

First, many shooters still believe overstabilizing bullets results in poor accuracy, but today’s well-balanced bullets shoot very well even when used in “too much” twist – which increases BC, important in longer-range shooting. Many shooters also believe the BC of a given bullet is a fixed number, when in fact it’s pretty flexible and with high-BC bullets increases with both velocity and rifling twist.

The symbol “Sg” is shorthand for gyroscopic stability. An Sg of 1.0 means a bullet is just barely stabilized, but overstabilizing a bullet up to 1.5 Sg increases ballistic coefficient by up to 15 percent, so the bullet flies flatter and drifts less in the wind.

Another common misconception is that bullets destabilize as velocity drops, resulting in poorer accuracy at longer ranges. Many shooters have “proven” this to themselves by shooting at longer ranges, finding their one-inch groups at 100 yards often expand not to 4 inches at 400 yards but to 8 or 10 inches.

Even into the 1980s, some companies used the original 1:14 twist for the .250 Savage, the reason John used the relatively short Speer 100-grain bullet in his Winchester Model 70 Lightweight. The bullet was probably just barely stabilized on this cold day.

In reality, bullets become more stable as range increases. A bullet’s spin slows only slightly as it flies through the air, while velocity drops rapidly, resulting in far less air pressure on the front of the bullet. The exception is when velocity drops to around the speed of sound, about 1,100 fps at sea level, but very few spitzers from modern hunting cartridges slow to “transonic” velocities within 800 yards, and most don’t until beyond 1,000 yards.

Instead, the major reason for larger groups at longer ranges is wind. Wind drift increases at approximately four times the rate of range, and most hunters aren’t very good at “reading” wind or compensating for its effects. As an example, a one-mph breeze (which most hunters would call absolutely calm) results in about 1.5 inches of wind drift at 400 yards with a typical 180-grain bullet from a .30-06, and a relatively mild but inconsistent breeze of one to 4 mph will increase a 400-yard group’s size by up to 5 inches.

The Miller formula isn’t as accurate with flat-based bullets, which stabilize in slightly slower twists than predicted, probably because of extra drag on the rear of the bullet. It agrees, however, with the Greenhill formula that a 500-grain .458 bullet measuring 1.25 inches long stabilizes in a 1:25 twist, even at the typical black-powder muzzle velocity of 1,200 fps.

At the other extreme, Don Miller eventually decided the pointy plastic tips on many long-range bullets are so light they shouldn’t be fully included in a bullet’s overall length. As an experiment, I clipped the plastic point from a Nosler .30-caliber, 180-grain Ballistic Tip, and on my Redding scale it weighed 2.0 grains. Then I clipped off an equal length from the tip of a Berger hollowpoint 185-grain Hunting VLD. The lead core doesn’t extend into the tip in VLDs, yet just that short length weighed 7.0 grains, three-and-a-half times as much as the plastic tip. Obviously the difference would be even more with the lead tip of a softpoint bullet.

Using the Miller formula helped me arrive at another useful twist statistic. Most rifling twists for modern, high-BC bullets range from 1:8 to 1:10, depending on caliber. Within that typical range, 5,000 feet in elevation is the equivalent of about an inch of rifling twist. Thus, a bullet the formula predicts will fully stabilize at sea level in a 1:8 rifling twist will perform about the same at 5,000 feet above sea level with a 1:9 twist, and at 10,000 feet in a 1:10 twist. I’ve confirmed this by shooting a bunch of bullets in rifles with varying rifling twists at various elevations in Montana. It’s why a handload with Berger 115-grain VLDs works pretty well in the 1:9 twist of my Ruger American .243 Winchester in my corner of the state, where even in the valleys, elevation averages around 5,000 feet. I wouldn’t take that load to South Texas.

Modern Twist Formula Notes